Wolfram`QuantumFramework`
QuantumCircuitOperator |
|
| | ||||
Details and Options
Examples
(26)
Basic Examples
(10)
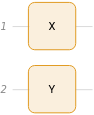
Create a quantum circuit composed of only single qubit gates:
In[1]:=
qc=
["X"],
["Y",{2}];
QuantumCircuitOperator |
QuantumOperator |
QuantumOperator |
Draw the associated circuit diagram:
In[2]:=
qc["Diagram"]
Out[2]=

Note the above circuit has a shorthand representation, too:
In[3]:=
QuantumCircuitOperator |
Out[3]=
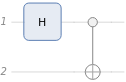
Create a circuit with multi-qubit gates:
In[1]:=
qc=
["CNOT"],
[{"H",2}];
QuantumCircuitOperator |
QuantumOperator |
QuantumOperator |
Associated circuit diagram:
In[2]:=
qc["Diagram"]
Out[2]=

Note the above circuit has a shorthand representation, too:
In[3]:=
QuantumCircuitOperator |
Out[3]=
True
Create circuits using the named ones.
Bell circuit:
In[1]:=
QuantumCircuitOperator |
Out[1]=
The Toffoli circuit:
In[1]:=
QuantumCircuitOperator |
Out[1]=

For the quantum Fourier circuit, we have with n the number of qubits. For example, the Fourier circuit of 2-qubits:
QuantumCircuitOperator[{"Fourier",n}]
In[1]:=
QuantumCircuitOperator |
Out[1]=

Fourier circuit of 5-qubits:
In[2]:=
QuantumCircuitOperator |
Out[2]=

For the quantum phase estimation, we have which takes two input arguments: a unitary operator U, and an integer n. The integer n specifies the number of qubits and operators in the circuit, with j=0,1,…,n-1. The accuracy of phase estimation and the success probability depends on n.
QuantumCircuitOperator[{"PhaseEstimation",u,n}]
controlled-
j
U
In[1]:=
QuantumCircuitOperator |
QuantumOperator |
Out[1]=

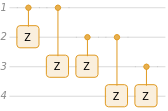
Given a graph, the corresponding circuit (which generates quantum graph/cluster states) is a series of controlled-Z operators on edges of graph:
In[1]:=
Graph[RandomGraph[{4,5}],VertexLabels"Name"]
Out[1]=

In[2]:=
QuantumCircuitOperator |
Out[2]=
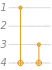
For the Bernstein–Vazirani algorithm, one needs to specify a secret string bit as s as follows: for the oracle we have , and for the whole circuit e . For example, the Bernstein–Vazirani oracle for the secret bit of 101:
QuantumCircuitOperator[{BernsteinVaziraniOracle,s}]
QuantumCircuitOperator[{BernsteinVazirani,s}]
In[1]:=
QuantumCircuitOperator |
Out[1]=
The Bernstein–Vazirani circuit for the secret bit of 101:
In[2]:=
QuantumCircuitOperator |
Out[2]=

Boolean oracle for a given Boolean function:
One can also get the decomposition of a Boolean oracle, in terms of CNOTs and Z-rotation:
For the diffusion part of the Grover circuit (also called, the amplification part), one only needs to specify the number of qubits:
Another way of storing the solution of a Boolean function is to save it as a phase, rather than on an ancillary qubit. This can be archived by using a phase oracle, that add an overall phase of π if the quantum state is a solution of the Boolean function.
The corresponding diffusion part, given a phase oracle:
One can also create the overall Grover circuit, using controlled-1 gates and a Boolean oracle:
One can also create the overall Grover circuit, using controlled-0 gates and a Boolean oracle:
One can also create the overall Grover circuit, using controlled-1 gates and a phase oracle:
One can also create the overall Grover circuit, using controlled-0 gates and a phase oracle:
One can find Trotter-Suzuki decomposition, to approximate a time evolution.
First order, only:
2nd order:
2nd order, with 4 steps:
4th order, only 1 step: