Towards Proving Causal Invariance in the Wolfram Model
Towards Proving Causal Invariance in the Wolfram Model
Silas K Grossberndt
City University of New York, Graduate Center
This project is directed at adding additional functionality to existing proof strategies for Wolfram Models. This work focuses on utilizing homotopies and ∞-groupoids to approach this proof, first moving out from an empirical study of a property and then to causal invariance. This work is not fully rigorous at this time, and these methods need to be supported with proof of the methods to either support them or lead to better refinement. Further work in this area would include probing into the structure of the groupoids from the causal graphs to extract additional properties of the models.
Introduction and Definitions
Introduction and Definitions
Theorem Proofs and Type Theory
Theorem Proofs and Type Theory
The goal of this project is to extend the existing functions for theorem proofs on multiway systems in the Wolfram Model to a broader spectrum of rules. One hopes to show that a rule will give causal invariance, rather than showing that two hypergraphs are invariant, but that all hypergraphs in the multiway system resulting from the rules will reconverge on the hypergraph.
This will be addressed by elevating the logics in the theorem provers to a type theoretic method, and exploit the ∞-groupoid structure of the causal graphs.
Definitions and Basis
Definitions and Basis
One starts with the correspondence from homotopy type theory of an ∞-groupoid to a space in a homotopy via the Curry-Howard-Lambek Correspondence. Then extend this correspondence to a type. Then, a proof corresponding to the theorem simply requires that one find an element of the appropriate groupoid, or a point in the appropriate space. This is generally true for the meta mathematics, and will provide the proper mathematical underpinnings for a rigorous definition of the presented system. However, in this work I shall go off of the basis used in the current “FindWolframModelProof” function, taking an assumption of the multiway systems as types, and then building from there. The presented work is meant to be treated as an experimental approach, empirically lead, but shall be developed on. The underlying idea is that those multiway systems that admit higher homotopies are those that will have a topological structure allowing for the analysis of causal invariance.
We shall use the following from [4]:
We shall use the following from [4]:
Homotopy
Homotopy
A homotopy is a map that maps from two paths such that H(I, 0)= f and H(I, 1)=g. If there exists a homotopy from f to g, then f and g are homotopic.
H:IIX
f,g:IX
Simply Connected Space
Simply Connected Space
A space is simply connected if it is path connected and has a trivial fundamental group from any basepoint in the space.
Path Connected Space
Path Connected Space
A path connected space is one where there is a path between any two points in the space.
Fundamental Group
Fundamental Group
The fundamental group, (X,) is the set of equivalence classes of loops, i.e. paths such that , with the group action as the composition of loops.
π
1
x
0
f:IX
f(0)f(1)
x
0
∞-Groupoid
∞-Groupoid
For this, I shall be using the refined definition of a ∞-groupoid from [1] which is just a further development of Grothendieck’s definition in [2] .
Then, when I shall be talking about the ∞-groupoid of the space, it shall specifically be the fundamental ∞-groupoid of the space.
This is to say that, for a topological space X, there is an associated fundamental ∞-groupoid built from the Whitehead Tower.
Then, when I shall be talking about the ∞-groupoid of the space, it shall specifically be the fundamental ∞-groupoid of the space.
This is to say that, for a topological space X, there is an associated fundamental ∞-groupoid built from the Whitehead Tower.
A First Property
A First Property
Take a rule with the form -> and let it run for ten steps
2
2
2
4
In[]:=
RulePlot[testmodel]testmodel["FinalStatePlot"]
Out[]=
Out[]=
In[]:=
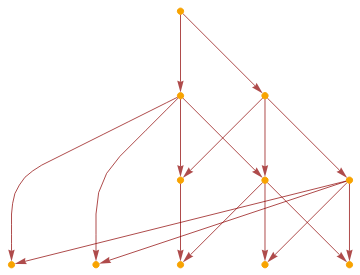
testmodel["CausalGraph"]//TransitiveReductionGraph//GraphPlot3D
Then, the resultant multiway systems and causal multiway systems after 4 steps are
In[]:=
multiwaytestmtcg//TransitiveReductionGraph
Let us start with taking two hypergraphs on the Multiway System and showing their equivalence, then from there lift out to non-enumerative methods on the causal multiway system
In[]:=
testmodel[1]
Out[]=
{{0,0},{0,1},{0,1},{0,1}}
In[]:=
multiwayproof=ResourceFunction["FindWolframModelProof"][testmodel[1]<->testmodel[2],{{x,y},{x,z}}<->{{x,w},{x,z},{z,w},{y,w}}];
In[]:=
multiwayproof["ProofGraph"]/."WolframModelLogic"->"EquationalLogic"
In[]:=
multiwayproof["ProofNotebook"]/."WolframModelLogic""EquationalLogic"
In[]:=
simpleproof=ResourceFunction["FindWolframModelProof"][{{0,0},{0,0}}<->{{0,0},{0,1}},{{x,y},{x,z}}{{x,z},{z,w},{y,w},{x,w}}]/."WolframModelLogic"->"EquationalLogic"
Now let us investigate these equivalences on the multiway graph.
We can see that the proof as given on the multiway system is relatively simple if we take two states that are direct evolutions in the original model. If we were to take two hypergraphs that were not as closely related, one would get
Now let us start with a property and test methodologies of getting to the property via the causal graph.
Growth of the Hypergraph
Growth of the Hypergraph
Let us take out test model and find a description of the growth from one state to another on the causal graph. Then, we will use other simple rules to verify that the
In[]:=
testmodel["FinalStatePlot"]
Out[]=
In[]:=
testmodel["CausalGraph"]//TransitiveReductionGraph//GraphPlot3D
Out[]=
Then take an earlier state of this causal graph
In[]:=
testmodelat4=ResourceFunction["WolframModel"][ru,{{0,0},{0,0}},4];
In[]:=
testmodelat4["CausalGraph"];
In[]:=
cg4=%;
In[]:=
cg4//TransitiveReductionGraph
Out[]=
In[]:=
testmodelat4["FinalStatePlot"]testmodel["FinalStatePlot"]
Out[]=
It is apparent that this hypergraph is growing from state to state. Then let us compare the causal graphs, multiway systems and causal multiway systems
If we take the homotopy class for path γ, we get that it is trivial as is the homotopy class for some η . This is to be expected, however the same is not true in the case of the causal multiway systems, which we shall get into in the next section.
Then, one notices that if the paths shown are chosen, there is an alternative path to get to the same end point, and thus there exists at least one non-trivial homotopy class.
Alternatively, before we can take this as a given for this property, let us investigate a rule that does fail to grow ad infinitum .
Then take the path δ below, and find that there are no homotopic paths
This may seem to be an ad-hoc approach, but this is expected to be mathematically rigorous, as, for the hypergraph to grow continuously, one would expect a homotopic structure
Then, to get this property on some rule and some initial state, one needs to simply verify that there is a path that is homotopic to an other path. This is just seeing that the space is not simply connected (a concept which will become useful in the next part of this project).
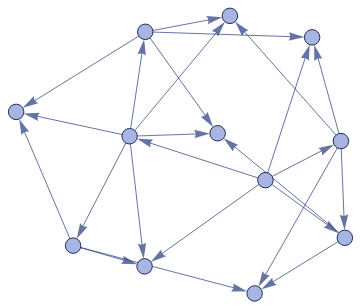
Then take the multiway system below
One notes that it is not possible to see at this point if the homotopies exist, but it can be shown (by inspection) that the fundamental groupoid on both the multiway system and the causal multiway system is trivial, and that they are path connected, so we do still get a homotopy class that spans the space, just trivially.
Causal Invariance
Causal Invariance
Let us now turn our attention to causal invariance. We shall try to show causal invariance by showing confluence on the causal multiway system and, alternatively, by showing that there must be an isomorphism from one causal graph to another and that all such morphisms are isomorphisms, i.e. showing that the ∞-groupoid exists and is non-trivial. The equivalence of these methods is not necessarily clear, and the methods presented here to get to each are a primary approach to each, needing further work to sufficiently prove that these methods are fully rigorous.
Both of these methods are in a resource function “ProveWolframModelCausalInvariance” uploaded to the function repository.
Confluence on the Causal Multiway System
Confluence on the Causal Multiway System
In the previous section, we had investigated how hypergraphs grow ad infinitum and had come to the conclusion that there would be at least one path on the system that had a trivial homotopy class at all foliations. This corresponds to a lack of confluence, as there would always be at least one path by which there would be a branch that would not recombine. Then, we note that causal invariance is given in the Technical Introduction to the Wolfram Physics Project [3] as confluence, or “path independence” [5] on the rewriting system, which we here extend to the causal multiway systems. Then, begin with a causal multiway system, one must show that, for all vertices that are not termini on the causal multiway system, each point must be within a path that is homotopic to at least one path for each other vertex on the causal multiway system. This is equivalent to saying that there must be, at some layer of foliation, for path γ, the homotopy class [[γ]] will be non-trivial and, in fact should span the space of all paths in the system. We choose Causal Multiway systems as they most clearly have the connection between confluence and causal invariance [6] [7]
Take a simple causal multiway system that has been shown to have causal invariance [3], and choose a path γ
Then, taking path γ, there is a single homotopy class for the whole space iff the space is simply connected. This can be gotten by proving that the space is path connected, which we will take as an assumption of the model, and that the fundamental group for all points is trivial. It is clear that for the termini points, all the paths to those points have a trivial fundamental group, however, it is less clear for paths like γ. For these, one must show that the fundamental group is trivial, which is a non-tractable problem in general. Instead, let us lift the problem to one of the fundamental groupoid. To prove that this is trivial, one must show that the space is contractible. This can be implemented using the method outlined in [8]
Isomorphisms on Causal Graphs
Isomorphisms on Causal Graphs
In an other method, one can instead take the multiway systems and prove that the fundamental ∞-groupoid from the paths in the multiway system is non-trivial, again using the method in [8] combined with a path lifting. Not every multiway system permits this groupoid structure, but those that do exhibit causal invariance. Groupoid structures can then be extracted to get additional properties.
Conclusion and further Extensions
Conclusion and further Extensions
This work needs to have a few proofs fleshed out, but right now the system relies on identification of an isomorphism for simple hypergraphs, such that the loop properties may be exploited for the fundamental groupoids. Getting exact structures would be a natural next step, as well as rewriting of the proof object to move from comparison of hypergraphs to rules, to comparison of paths and spaces to the rules. However, this work is expected to fit within the larger project of higher logic proofs on the Wolfram Model.
Keywords
Keywords
◼
WolframPhysicsProject
◼
Causal Invariance
◼
Automated Theorem Proving
◼
Homotopy Type Theory
Acknowledgment
Acknowledgment
My thanks to my mentor Nikolay Murzin for his support on this project. Additional thanks go to Stephen Wolfram and Jonathan Gorard for suggestion of the project topic, and to Mano Namuduri and Xerxes Arsiwalla for important discussions on homotopy type theory, the Wolfram Model and getting notebooks to look the way I wanted them too.
References
References
◼
[1] G. Maltsiniotis arXiv:1009.2331 [math.CT]
◼
[2]A. Grothendieck and Édité par G. Maltsiniotis. “Pursuing Stacks.” (2010).
◼
[3] S. Wolfram “ A Class of Models with the Potential to Represent Fundamental Physics” https://www.wolframphysics.org/technical-introduction/the-updating-process-for-string-substitution-systems/the-phenomenon-of-causal-invariance/
◼
[4] L. Evans and R. Tompson, “Algebraic Topology” http://math.hunter.cuny.edu/thompson/topology_notes/chapter%20two.pdf
◼
[5] A. Church and J. B. Rosser (1936), “Some Properties of Conversion”, T Am Math Soc 39, 472–82. doi:10.1090/S0002-9947-1936-1501858-0.
◼
[6] J. Gorard arXiV:2004.14810
◼
[7] J. Gorard arXiV:2011.12174
◼
[8] D. O. Martinez-Rivillas and Ruy J.G.B de Queiroz, arXiV: 1906.05729v3[cs.Lo]
Initialization Cells
Initialization Cells