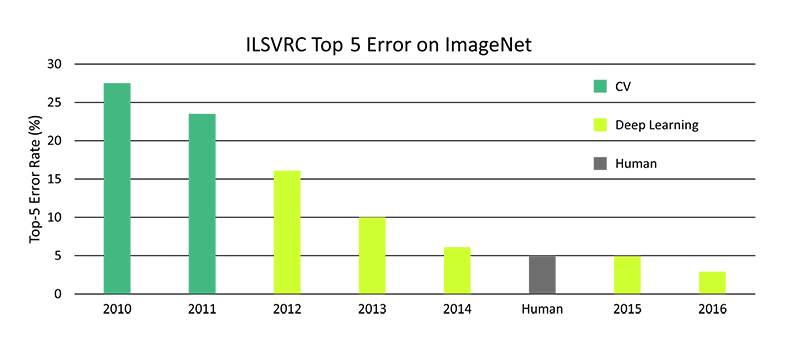You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
What is Deep Convolution Neural Network?
Seriously?! You never heard about Deep Convolution Neural Networks, have't you?
The Deep Convolution Neural Networks are state of the art algorithms in many Computer Vision problems such as image classification or detection.
The Deep Convolution Neural Networks are state of the art algorithms in many Computer Vision problems such as image classification or detection.
Ooww come on! State of the art algorithm? What do you mean by this?
Have you heard about ImageNet Large Scale Visual Recognition Challenge (ILSVRC)?
Probably not. The goal of this competition is to predict one of the 1000 class which describes the image.
Please, take a look at the competition results over time.
Probably not. The goal of this competition is to predict one of the 1000 class which describes the image.
Please, take a look at the competition results over time.
As you see since 2012 there is a huge improvement of the detection algorithms performance.
Hmmm. Ok, fine! So you mentioned about Deep Neural Network? How does it work?
Generally, this model have a formulation that can map your input , all the way to the target objective, via a series of hierarchically stacked (this is where the' deep' comes from) operations.
Those operations are typically linear operations/projections (), followed by a non - linearities (), like so
x
y
Those operations are typically linear operations/projections (
W
i
f
i
y=(…(()))
f
N
f
2
f
1
T
x
W
1
W
2
…W
N
(
1
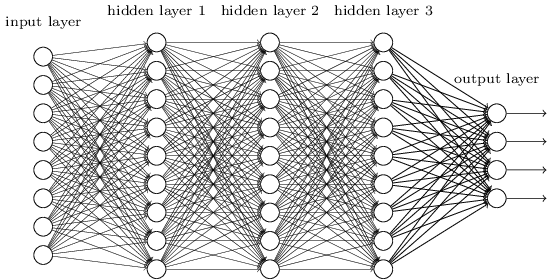
)The one of the most traditional and easiest to understand DL architecture is known as a multi - layer perceptron, (MLP). In that kind of network every element of a previous layer, is connected to every element of the next layer. It looks like this :
Ohhh! I've just realize something.
You said “every element of a previous layer was connected to the every element of a next layers”.
So, let assume our input is 10D and we have first layer of 20 hidden units. So in this very basic example∈ and that’s mean a lots of weights to be tuned.
How about the images?! The simple image is a NxM matrix so your input is dimensional e.g. small image (64x64 pixels) tends to generates input of 4096D! Deal with it!
You said “every element of a previous layer was connected to the every element of a next layers”.
So, let assume our input is 10D and we have first layer of 20 hidden units. So in this very basic example
W
1
10x20
R
How about the images?! The simple image is a NxM matrix so your input is
N·M
Yes! you are definitely right.
The MLP model is not designed to work with images. Nevertheless, It is very usefully when you working on categorical data and your input is low dimensional.
The MLP model is not designed to work with images. Nevertheless, It is very usefully when you working on categorical data and your input is low dimensional.
Ok, fine. So how about the images?
Do you know any other DL architectures designed for analyzing images?
Do you know any other DL architectures designed for analyzing images?
“PATIENCE YOU MUST HAVE my young padawan”
Before we move to convolution networks I would like to explain to you the idea of convolution operation.
Before we move to convolution networks I would like to explain to you the idea of convolution operation.
Lets start from the basic. What is convolution?
Convolution is the process of adding each element of the image to its local neighbors, weighted by a kernel. This is related to a form of mathematical convolution.
;
For example, the element at coordinates [2,2] (that is, the central element) of the resulting image would be calculated in the following way:
Convolution is the process of adding each element of the image to its local neighbors, weighted by a kernel. This is related to a form of mathematical convolution.
;
For example, the element at coordinates [2,2] (that is, the central element) of the resulting image would be calculated in the following way:
a | b | c | d | e |
f | g | h | i | j |
k | l | m | n | o |
p | q | r | s | t |
u | v | x | y | z |
|
|
(
2
)I suppose you noticed that this operation time complexity for MxN images and kxk kernel is .
O(MNkk)
Now, I would like to show you a couple of examples of different kernels.
But first I need to import exemplary image. I take image of Lena. It the name given to a standard test image widely used in the field of image processing since 1973.
But first I need to import exemplary image. I take image of Lena. It the name given to a standard test image widely used in the field of image processing since 1973.
Lena=ImageResize[ExampleData[{"TestImage","Lena"}],200]
The first kernel - identity one.
ImageConvolveLena,
0 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
I know this was trivial operation.
Now, let’s take a look at more interesting example - Edge detection.
BinarizeImageConvolveLena,
0 | 1 | 0 |
1 | -4 | 1 |
0 | 1 | 0 |
Pretty impressive hmm?! How about blurring? It is very usefully when you want to remove noise from the image.
Take a look at the cell below. You can apply different kind of noises and then try to remove it via applying gaussian filter.
Take a look at the cell below. You can apply different kind of noises and then try to remove it via applying gaussian filter.
Manipulate[ImageConvolve[ImageEffect[Lena,{noiseType,amoundOfNoise}],GaussianMatrix[radius]],{noiseType,{"Noise","GaussianNoise","PoissonNoise","SaltPepperNoise"}},{amoundOfNoise,0,0.99},{radius,1,10,1}]
Wow Dude! That was awesome!
But, why are you talking about this. You suppose to present Neural Networks!
But, why are you talking about this. You suppose to present Neural Networks!
As you see the convolution filters are very powerful tool. But we need to figure out the kernel size and parameters.
This is not a trivial task. It would be very nice if we found a way to somehow learn this weights.
Here comes Deep CNN. Exemplary architecture of that kind of network is presented below.
On demand I can add a short introduction to pooling and nonlinearity layers.
This is not a trivial task. It would be very nice if we found a way to somehow learn this weights.
Here comes Deep CNN. Exemplary architecture of that kind of network is presented below.
On demand I can add a short introduction to pooling and nonlinearity layers.
Master please show me some example.
How to build and train that kind of network?
How to build and train that kind of network?
Yes sure. In the purpose of this example I will use MNIST dataset. It is a large database of handwritten digits.
The MNIST database contains 60,000 training images and 10,000 testing images.
The MNIST database contains 60,000 training images and 10,000 testing images.
We have a dataset. That’s good.
Now let’s construct Shallow Convolution Neural Network. Our network contains only two hidden Convolution Layers.
You will see this architecture allows us to obtain great result.
Now let’s construct Shallow Convolution Neural Network. Our network contains only two hidden Convolution Layers.
You will see this architecture allows us to obtain great result.
Now it is time to train our network.
Here comes my question. How can I preserve learning curve plots? How can I visualize gradient flow?
Here comes my question. How can I preserve learning curve plots? How can I visualize gradient flow?
Now I want to check the network performance. At first basic test. Let take a look at first 100 test events.
Above test is a very naive. We are not able to look at each of the test examples. We need to do something a little bit smarter.
We can based our judgment on classifier performance measurement metrics accuracy.
Accuracy is a description of systematic errors, a measure of statistical bias; as these cause a difference between a result and a “true” value.
In other words it gives you a ratio of correctly classified example to all of the test examples. So the best possible value, perfect classification, is 1.
We can based our judgment on classifier performance measurement metrics accuracy.
Accuracy is a description of systematic errors, a measure of statistical bias; as these cause a difference between a result and a “true” value.
In other words it gives you a ratio of correctly classified example to all of the test examples. So the best possible value, perfect classification, is 1.
What does this result mean?
It basically tells you that this classifier in roughly 99% returns correct prediction.
Another way of looking at the classifier performance is so called confusion matrix. Each column of the matrix represents the instances in a predicted class while each row represents the instances in an actual class.The name stems from the fact that it makes it easy to see if the system is confusing two classes (i.e. commonly mislabelling one as another).
It basically tells you that this classifier in roughly 99% returns correct prediction.
Another way of looking at the classifier performance is so called confusion matrix. Each column of the matrix represents the instances in a predicted class while each row represents the instances in an actual class.The name stems from the fact that it makes it easy to see if the system is confusing two classes (i.e. commonly mislabelling one as another).