You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Artificial Neural Networks
Artificial Neural Networks
An Artificial Neural Network (ANN) is a computing system which is similar to a biological neural network. These systems learn to do tasks by considering examples, generally without task specific programming.
Origins of Neural Networks
Warren McCulloch and Walter Pitts created a computational model for neural networks based on mathematics and algorithms called threshold logic. This led to research for Neural network to split into two approaches, one was focused on the biological processes in the brain while the other focused on the application of neural networks to AI.
Rosenblatt in 1958 created the perceptron, an algorithm for pattern recognition. With mathematical notation, Rosenblatt described circuitry not in the basic perceptron, such as the exclusive-or circuit.
Neural network research stagnated after machine learning research by Minsky and Papert, who discovered two key issues with the computational machines that processed neural networks. The first was the basic perceptrons were incapable of processing the exclusive-or circuit. The second was that computers didn’t have enough processing power to effectively handle the work required by large neural networks. Neural Network research slowed until computers achieved far greater processing power.
Rosenblatt in 1958 created the perceptron, an algorithm for pattern recognition. With mathematical notation, Rosenblatt described circuitry not in the basic perceptron, such as the exclusive-or circuit.
Neural network research stagnated after machine learning research by Minsky and Papert, who discovered two key issues with the computational machines that processed neural networks. The first was the basic perceptrons were incapable of processing the exclusive-or circuit. The second was that computers didn’t have enough processing power to effectively handle the work required by large neural networks. Neural Network research slowed until computers achieved far greater processing power.
Section
Section
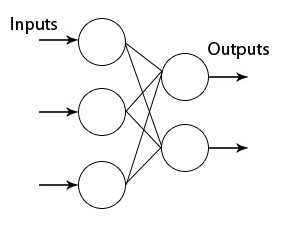
The neurons are organized in layers where the signals travel from a set of inputs to the last set of outputs after traversing successively all the layers.
◼
Let’s have a look at the topology of the network.
In[97]:=
Import["http://neuroph.sourceforge.net/tutorials/images/perceptron.jpg","Image"]
Out[97]=
In the Wolfram Language we can use the NetGraph symbol. It can be used to specify a neural net defined by a graph in which the output of layer is given as input to layer .
m
i
n
i
◼
Create a net with one layer:
In[95]:=
neuralnet=NetGraph[{ElementwiseLayer[Ramp]},{}]
Out[95]=
NetGraph
◼
Create a net with two layers whose output vectors are 3 and 5.
In[79]:=
net=NetGraph[{LinearLayer[3],LinearLayer[5]},{12},"Input"2]
Out[79]=
NetGraph
◼
Initialize all arrays in the above net and give numeric inputs to the net:
In[80]:=
net=NetInitialize[net];
In[81]:=
net[{1.0,2.0}]
Out[81]=
{-0.541849,-0.167301,-0.0138126,-0.338522,-0.549727}
◼
Create a linear layer whose output is a length-5 vector :
In[82]:=
LinearLayer[5]
Out[82]=
LinearLayer
The above linear layer cannot be initialized until all its input and output dimensions are known. The LinearLayer is a trainable, fully connected net layer that computes only the output vector of size n.
Create a randomly initialized LinearLayer :
Create a randomly initialized LinearLayer :
In[83]:=
linear=NetInitialize@LinearLayer[5,"Input"3]
Out[83]=
LinearLayer
In[84]:=
linear[{1,2,1}]//MatrixForm
Out[84]//MatrixForm=
-0.741161 |
-0.867255 |
-0.843027 |
1.48873 |
0.266249 |
The linear function was used to call 3 inputs which gave a matrix vector of 5 elements, i.e because we initialized a linear layer of 5 outputs.
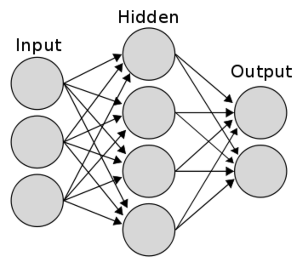
In[98]:=
Import["https://www.researchgate.net/profile/Haohan_Wang/publication/282997080/figure/fig4/AS:305939199610886@1449952997594/Figure-4-A-typical-two-layer-neural-network-Input-layer-does-not-count-as-the-number-of.png","Image"]
Out[98]=
The above is a representation of a 2 layer neural network.
◼
Let’s make our own Neural Network and use that to classify the MNIST handwritten digits.
We will first load the data, and we will take 5000 examples as training data and 1000 examples as test data.
We will first load the data, and we will take 5000 examples as training data and 1000 examples as test data.
In[85]:=
resource=ResourceObject["MNIST"];trainingDataImg=RandomSample[ResourceData[resource,"TrainingData"],5000];testDataImg=RandomSample[ResourceData[resource,"TestData"],1000];
In order to train the example we take the pixel values of the image and flatten them into a list, as for the digits, we change them into 10x1 vectors, with the corresponding index setting to be 1.
In[88]:=
rule=Rule[x_,y_]:>Flatten[ImageData[x]]->(If[#==y+1,1,0]&/@Range[10]);trainingData=trainingDataImg/.rule;testData=testDataImg/.rule;
Now we can construct the neural network. We will use three layers of (28*28), 30, and 10 neurons. Each neuron will be activated by the sigmoid function :
In[90]:=
lenet=NetChain[{(*secondlayer*)DotPlusLayer[30],ElementwiseLayer[LogisticSigmoid],(*thirdlayer*)DotPlusLayer[10],ElementwiseLayer[LogisticSigmoid]},"Input"784]
Out[90]=
NetChain
◼
Let's train this!
In[91]:=
trained=NetTrain[lenet,trainingData,MaxTrainingRounds150]
Out[91]=
NetChain
◼
Let' s test it out!
In[92]:=
Counts[testData/.Rule[x_,y_]First@Flatten[Position[#,Max[#]]&@trained[x]]-1First@Flatten@Position[y,1]-1]
Out[92]=
False110,True890
We get an accuracy of 89% with a 3 layer neural network.
◼
Convolutional Neural Network
Convolution neural networks (CNN) were inspired by biological processes in which the connectivity pattern between neurons is inspired by the organization of the animal visual cortex.
Convolution neural networks (CNN) were inspired by biological processes in which the connectivity pattern between neurons is inspired by the organization of the animal visual cortex.
In[28]:=
Import["https://qph.ec.quoracdn.net/main-qimg-cc30aa65a662315c3c22e405722c4109","Image"]
Out[28]=
Convolutional Layer
Convolutional Layer
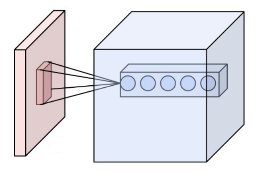
The convolutional layer is the foundation of the CNN. The layer’s parameters consists of a set of learnable filters or kernels which have a small receptive field. During the forward pass, each filter is convolved across the width and height of the input volume, computing the dot product between the entries of the filter and the input and producing a 2 dimensional activation map of that filter. As a result, the network learns filters that activate when it detects some specific type of feature at some position in the input.
In[101]:=
Import["https://upload.wikimedia.org/wikipedia/commons/6/68/Conv_layer.png","Image"]
Out[101]=
Pooling Layer
Pooling Layer
Pooling is a form of non linear down - sampling. In pooling the input image is partitioned into a set of non overlapping rectangles and, for each sub region outputs the maximum. The intuition is that the exact location of a feature is less important than its rough location relative to other features, The pooling layer serves to progressively reduce the spatial size of the representation, to reduce the number of parameters and amount of computation in the network and hence also control over-fitting. It is common to periodically insert a pooling layer between successive convolutional layers in a CNN architecture.
◼
Create a one-dimensional Convolution Layer with 2 output channels and a kernel size of 4.
◼
Create an initialized one dimensional Convolution Layer :
◼
Let’s design a convolution neural network for recognizing handwritten digits.
◼
Let’s train the network for three training rounds.
◼
Evaluate the trained network directly on images randomly sampled from the validation set.
◼
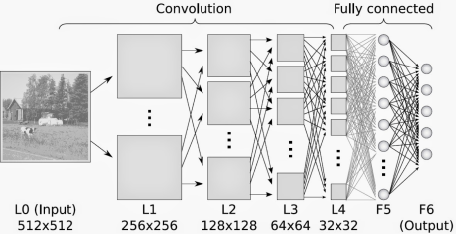
LeNet Architecture
Further Explorations
Recurrent Neural Networks
Differentiable Neural Computers
Authorship information
Aishwarya Praveen
23.06.17
anshu4321@gmail.com