3 jet fraction in the cross section for +e-ehadrons
3 jet fraction in the cross section for hadrons
+
e
-
e
Demonstration how to get this cross section from the lagrangian via different jet algorithms
Notation and rules
Notation and rules
◼
We use vec for vectors, g for the metric tensor and distinguish upper and lower indices:
In[84]:=
Format[g[a_,b_],TraditionalForm]:=Subscript[g,SequenceForm[a,b]]Format[g[up[a_],b_],TraditionalForm]:=Subsuperscript[g,b,a]Format[g[b_,up[a_]],TraditionalForm]:=Subsuperscript[g,b,a]Format[g[up[a_],up[b_]],TraditionalForm]:=Superscript[g,SequenceForm[a,b]]Attributes[g]=Orderless;Format[γ[a_],TraditionalForm]:=Format[γ[up[a_]],TraditionalForm]:=Format[vec[a_,b_],TraditionalForm]:=Format[vec[a_,up[b_]],TraditionalForm]:=vec[0,_]=0;
γ
a
a
γ
a
b
b
a
◼
We use SP for scalar product:
In[94]:=
SP[0]=0;Attributes[SP]=Orderless;SP[aa_,aa_]:=SP[aa]SP[aa_,-bb_]:=-SP[aa,bb]SP[-aa_]:=SP[aa]Format[SP[a_,b_],TraditionalForm]:=SequenceForm[a,b]Format[SP[a_],TraditionalForm]:=SP[0,_]=0;
2
a
◼
convolution rules
In[102]:=
gammasim={a___·γ[up[c_]]·γ[up[d_]]·b___vec[e_,c_]vec[e_,d_](-SP[e])a·b,g[a_,b_]vec[c_,up[b_]]vec[c,a],g[a_,up[b_]]vec[c_,b_]vec[c,a],g[a_,up[b_]]g[c_,b_]g[c,a],g[dd_,up[b_]]c___·γ[b_]·a___c·γ[dd]·a,g[dd_,b_]c___·γ[up[b_]]·a___c·γ[dd]·a,vec[ka_,b_]vec[c_,up[b_]]-SP[ka,c],g[ao_,up[ao_]]->4}
Out[102]=
a___···b___(-(a·b)),,,,c___··a___c··a,c___··a___c··a,-(cka),4
e_
c_
e_
d_
c_
γ
d_
γ
2
e
b_
c_
g
a_b_
c
a
c_
b_
b_
g
a_
c
a
g
b_c_
b_
g
a_
g
ac
b_
g
dd_
γ
b_
γ
dd
g
b_dd_
b_
γ
γ
dd
b_
c_
ka_
b_
ao_
g
ao_
γ-matrix trace (spur) calculation
γ-matrix trace (spur) calculation
We use the anticommutator relation for γ-matrices +=2 to express the trace of n γ-matrices through traces of n-2 γ-matrices:
a
γ
b
γ
b
γ
a
γ
ab
g
◼
Sp takes as argument the Lorenz indices of the γ-matrices and returns the trace
In[103]:=
Sp[a__]:=0/;OddQ[Length@{a}];Module[{a,b,c,d,e,f},Sp[a__]:=(b=f@@Range[Length[{a}]];b//.f[c___,1,d_,e___]g[1,d]f[c,e]-f[c,d,1,e]/.f[___,1]0/.Thread[List@@b{a}]/.fSp);]Sp[a_,bf_]:=4g[a,bf];
Example ]:
tr[
γ
a
γ
b
γ
c
γ
d
In[106]:=
Sp[a,b,c,d]
Out[106]=
4g[a,d]g[b,c]-4g[a,c]g[b,d]+4g[a,b]g[c,d]
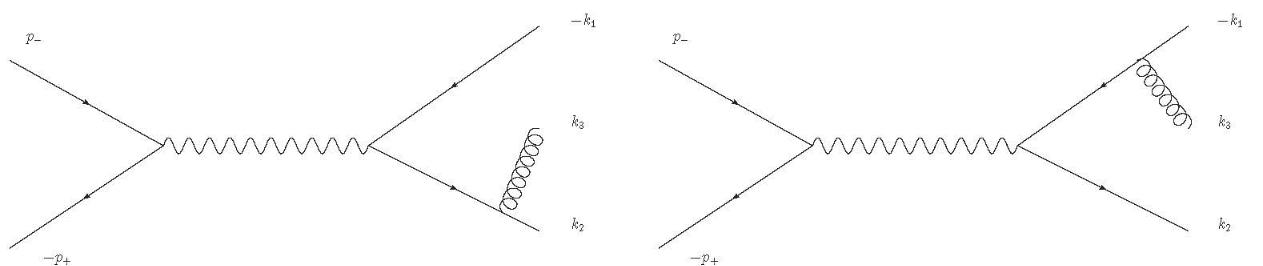
Cross section for q OverLine(q)-bargluon production
Cross section for q production
OverLine(q)-bargluon
◼
We have to calculate the sum of 2 diagrams
◼
The leptonic tensor cancels in the ratio of the 3 jet cross section and the LO 2 jet one. So we do not need it.
◼
The hadronic tensor reads
In[107]:=
ht=g[α,β]γ[up[κ11]]·-+·γ[up[κ22]]·-+vec[k1,κ11]vec[k2,κ22]
γ[up[α]]·(γ[up[κ2]]vec[k2,κ2]+vec[k3,κ3]γ[up[κ3]])·γ[up[μ]]
SP[k2+k3]
γ[up[μ]]·(γ[up[κ1]]vec[k1,κ1]+vec[k3,κ3]γ[up[κ3]])·γ[up[α]]
SP[k1+k3]
γ[μ]·(γ[up[κ222]]vec[k2,κ222]+vec[k3,κ33]γ[up[κ33]])·γ[up[β]]
SP[k2+k3]
γ[up[β]]·(γ[up[κ111]]vec[k1,κ111]+vec[k3,κ33]γ[up[κ33]])·γ[μ]
SP[k1+k3]
Out[107]=
γ[up[κ11]]·-·γ[up[κ22]]·-g[α,β]vec[k1,κ11]vec[k2,κ22]
γ[up[μ]]·(vec[k1,κ1]γ[up[κ1]]+vec[k3,κ3]γ[up[κ3]])·γ[up[α]]
SP[k1+k3]
γ[up[α]]·(vec[k2,κ2]γ[up[κ2]]+vec[k3,κ3]γ[up[κ3]])·γ[up[μ]]
SP[k2+k3]
γ[up[β]]·(vec[k1,κ111]γ[up[κ111]]+vec[k3,κ33]γ[up[κ33]])·γ[μ]
SP[k1+k3]
γ[μ]·(vec[k2,κ222]γ[up[κ222]]+vec[k3,κ33]γ[up[κ33]])·γ[up[β]]
SP[k2+k3]
◼
We expand this expression into a linear combination of γ-matrix products
In[108]:=
Attributes[CenterDot]:=Flat;ht1=ht/.γ[a_]CenterDot[γ[a]]//.a___·(b_CenterDot[c_]+d_CenterDot[e_])·f___b(a·c·f)+d(a·e·f)
Out[109]=
k1
κ11
k2
κ22
g
αβ
1
2
(k1+k3)
k3
κ3
k1
κ111
κ11
γ
μ
γ
κ3
γ
α
γ
κ22
γ
β
γ
κ111
γ
γ
μ
k3
κ33
κ11
γ
μ
γ
κ3
γ
α
γ
κ22
γ
β
γ
κ33
γ
γ
μ
2
(k1+k3)
k2
κ222
κ11
γ
μ
γ
κ3
γ
α
γ
κ22
γ
γ
μ
κ222
γ
β
γ
k3
κ33
κ11
γ
μ
γ
κ3
γ
α
γ
κ22
γ
γ
μ
κ33
γ
β
γ
2
(k2+k3)
k1
κ1
k1
κ111
κ11
γ
μ
γ
κ1
γ
α
γ
κ22
γ
β
γ
κ111
γ
γ
μ
k3
κ33
κ11
γ
μ
γ
κ1
γ
α
γ
κ22
γ
β
γ
κ33
γ
γ
μ
2
(k1+k3)
k2
κ222
κ11
γ
μ
γ
κ1
γ
α
γ
κ22
γ
γ
μ
κ222
γ
β
γ
k3
κ33
κ11
γ
μ
γ
κ1
γ
α
γ
κ22
γ
γ
μ
κ33
γ
β
γ
2
(k2+k3)
1
2
(k2+k3)
k3
κ3
k1
κ111
κ11
γ
α
γ
κ3
γ
μ
γ
κ22
γ
β
γ
κ111
γ
γ
μ
k3
κ33
κ11
γ
α
γ
κ3
γ
μ
γ
κ22
γ
β
γ
κ33
γ
γ
μ
2
(k1+k3)
k2
κ222
κ11
γ
α
γ
κ3
γ
μ
γ
κ22
γ
γ
μ
κ222
γ
β
γ
k3
κ33
κ11
γ
α
γ
κ3
γ
μ
γ
κ22
γ
γ
μ
κ33
γ
β
γ
2
(k2+k3)
k2
κ2
k1
κ111
κ11
γ
α
γ
κ2
γ
μ
γ
κ22
γ
β
γ
κ111
γ
γ
μ
k3
κ33
κ11
γ
α
γ
κ2
γ
μ
γ
κ22
γ
β
γ
κ33
γ
γ
μ
2
(k1+k3)
k2
κ222
κ11
γ
α
γ
κ2
γ
μ
γ
κ22
γ
γ
μ
κ222
γ
β
γ
k3
κ33
κ11
γ
α
γ
κ2
γ
μ
γ
κ22
γ
γ
μ
κ33
γ
β
γ
2
(k2+k3)
◼
and calculate the traces
In[110]:=
ht2=Expand[ht1/.cd__CenterDotSp@@cd〚All,1〛]//.gammasim
◼
take into account that the final particles are massless
Cross section for 3 jet production
Cross section for 3 jet production
◼
We define the phase space
◼
And draw the differential cross section
◼
Calculate the cross section as function of the jet algorithm parameter d
◼
Show all in one interactive output
Questions
Questions
Authorship information
Date of creation 20.06.2017
Author email address a.v.grabovsky@inp.nsk.su