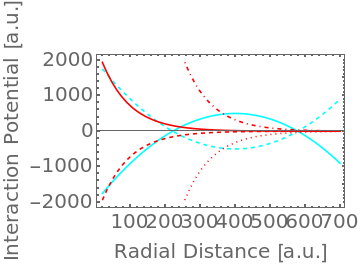
potNuTot[r_]:=potNu[scNu,stNu,r](2nu11[r]-1-as(2anu11[r]-1))(*simulatedtotalneutrinopotential*);Plot[{potBG[xBG,yBG,wBG,r](*backgroundpotential*),-potBG[xBG,yBG,wBG,r](*inverseofbackgroundpotential*),potNu[scNu,stNu,r]+potAnu[as,scNu,stNu,r](*totalneutrinopotentialwithbothelectrontypeneutrinoandantineutrino*),-potNu[scNu,stNu,r]-potAnu[as,scNu,stNu,r](*totalneutrinopotentialwithbothnon-electrontypeneutrinoandantineutrino*),potNu[scNu,stNu,r]-potAnu[as,scNu,stNu,r](*totalneutrinopotentialwithelectrontypeneutrinoandnon-electrontypeantineutrino*),-potNu[scNu,stNu,r]+potAnu[as,scNu,stNu,r](*totalneutrinopotentialwithnon-electrontypeneutrinoandelectrontypeantineutrino*),potNuTot[r](*simulatedtotalneutrinopotential*)},{r,rmin,rmax},PlotStyle{Cyan,{Cyan,Dashed},Red,{Red,Dashed},{Red,DotDashed},{Red,Dotted},Blue},FrameTrue,PlotRange{{rmin,rmax},{-1000,1000}},FrameTrue,PlotStyle{Cyan,{Cyan,Dashed},Red,{Red,Dashed},{Red,DotDashed},{Red,Dotted}},FrameLabel{"Radial Distance [a.u.]","Interaction Potential [a.u.]"},FrameTicksStyleThick,LabelStyleDirective[FontSize20],PlotLegends{"Background Potential","Inverse Background Potential","Neutrino Potential (both electron type)","Neutrino Potential (both non-electron type)","Neutrino Potential (electron neutrino, non-electron antineutrino)","Neutrino Potential (non-electron neutrino, electron antineutrino)","Simulated Neutrino Potential"}]