Insert
Sample

Euclidean Vector Introduction

A vector is a quantity that has both a magnitude and direction.

Vector Basics

Let’s start by making a vector in the 2-D Cartesian plane.
◼
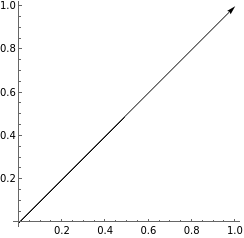
Draw the vector v starting at point (0,0) and ending at point (1,1).
In[6]:=
Graphics[{Arrow[{{0,0},{1,1}}]},AxesTrue]
Out[6]=
This vector describes a quantity that is pointed in the northeast direction. Its norm, or magnitude, is defined as
2
(
x
2
-
x
1
)
+
2
(
y
2
-
y
1
)
.
◼
Calculate the norm of v, or Norm[v].
In[408]:=
Sqrt[(1-0)^2+(1-0)^2]
Out[408]=
2
Thus the magnitude of this vector v (||v||) can be said to be
2
. This vector v would be written as {1,1} because it moves over 1 unit in the x direction and up 1 unit in the y direction.

Unit Vectors

Unit vectors are vectors that have a direction but have a magnitude of 1.
◼
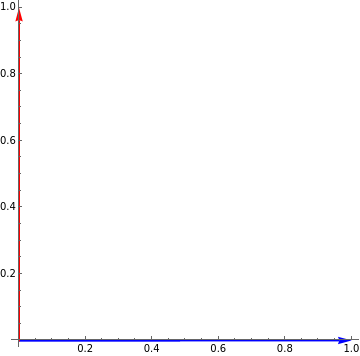
Show the unit vector i in blue and j in red.
In[103]:=
Graphics[{Blue,Thick,Arrow[{{0,0},{1,0}}],Red,Arrow[{{0,0},{0,1}}]},AxesTrue]
Out[103]=
The vector {1,1} could also be written as i + j where both terms have a coefficient of 1. Unit vector i corresponds to the x-component (horizontal) while j corresponds to the y-component (vertical).

Vector Decomposition

In order to begin vector operations, we need to know how to get its components.
◼
Find the vertical component of the vector {1,1}.
In[69]:=
Norm[{1,1}]*Sin[Pi/4]
Out[69]=
1
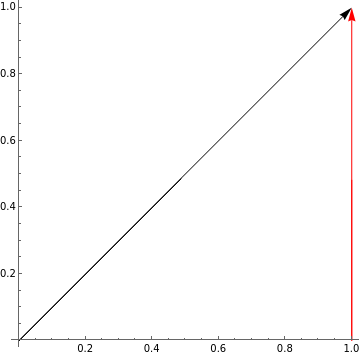
Using simple trigonometry by viewing the vector as a triangle’s hypotenuse, we can obtain the vertical component.
◼
Display the vertical component graphically.
In[74]:=
Graphics[{Arrow[{{0,0},{1,1}}],Red,Arrow[{{1,0},{1,1}}]},AxesTrue]
Out[74]=
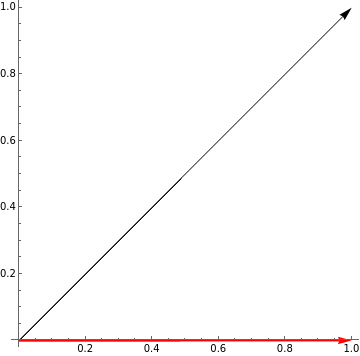
The horizontal component is very similar.
In[76]:=
Norm[{1,1}]*Cos[Pi/4]
Out[76]=
1
◼
Display the horizontal component graphically.
In[104]:=
Graphics[{Arrow[{{0,0},{1,1}}],Red,Thick,Arrow[{{0,0},{1,0}}]},AxesTrue]
Out[104]=
◼
Create your own vector and look at its components.
In[10]:=
Manipulate[​​Graphics[{​​Arrow[{{0,0},{a,b}}],​​Red,Thick,Arrow[{{0,0},{a,0}}],​​Blue,Arrow[{{a,0},{a,b}}]},​​PlotRange{{-10,10},{-10,10}},AxesTrue,​​Epilog{​​Text[Style[a,Red,FontSize20],{5,5}],​​Text[Style[b,Blue,FontSize20],{5,6}],​​Text[Style[Norm[{a,b}],Black,FontSize20],{5,7}]}],​​{a,-10,10,0.1},{b,-10,10,0.1}]
Out[10]=
​
a
b

Vector Addition and Subtraction

Just like scalars, which have only a magnitude and no direction, vectors can undergo operations such as addition and subtraction.
◼
Add the two vectors {3,2} and {0,4} together.
In a vector addition, individual components are added. We get {3,6} from {3+0, 2+4}. Subtraction works the same way.
◼
Subtract the vector {5,2} from the vector {1,3}.

Vector Multiplication: Dot Product

Multiplication of vectors is a bit more complex. We’ll start with the dot product. The result of a dot product is not a vector but instead is a scalar with just a magnitude and no direction. What it shows is the projection of vector one along vector two.
◼
Take the dot product of the vectors {4,1} and {2,1}.
It is obtained from 1*2 + 1*0.
◼
Without knowing the components of a vector, the dot product can be obtained by:
This is ||v||*||u||*cos(θ) where v and u are vectors and θ is the angle between them.
◼
Let’s look at it graphically:
From this we can easily see that there is no projection of the first vector onto the second vector that is along the y-axis, which is why in our dot product 1*2 + 1*0, the second term results in a 0.
◼
Like scalar multiplication, order does not matter for a dot product.

Vectors in 3-D

Just as vectors can exist in two dimensions, so they can exist in three dimensions.
◼
Draw the vector {1,1,1}.
◼
Find the norm of the vector v = {1,2,3}.
In three dimensions, addition and taking the dot product work the exact same way but with an added term. Additionally, the unit vector in the third dimension is k.
◼
Make your own 3-D vector.

Vector Multiplication: Cross Product

◼
The cross product takes two vectors and results in a vector that is orthogonal to both.
This time the output is a vector and not a scalar like the dot product.
◼
The magnitude of the cross product is the same as ||v||*||u||*sin(θ) where θ is the angle between the two vectors.
This is the same as
◼
Let’s see what these three vectors look like.
◼
The cross product is the same as finding the determinant of the matrix
where i, j, and k are the x, y, and z unit vectors respectively. The result of the cross product of vector {1,0,0} and {0,1,0} is {0,0,1}, or k.
◼
Unlike the dot product, the order of vectors in a cross product does matter.
◼
While order matters, the result of changing the order will be the same vector multiplied by -1.
◼
Now let’s do flip the order and multiply by -1.
We can see the results are the same. That’s all there is to know about basic Euclidean vectors!
Further Explorations
Parametric Equations of Vectors
Vector Fields
Tangent Vectors
Authorship information
Ethan Truelove
19 June 2017
ethan.truelove@me.com