Time Dilation

​
Vector Addition

In every day life, velocities of objects add like vectors. This means that the velocity of an object that you observe depends not only on the objects motion, but on your own motion as well.
◼
  • V
    AC
    =
    V
    AB
    +
    V
    BC
    • Graphics[Arrow[{{0,0},{2,0}},{0,1}]]​​Style["+",40,Bold]​​Graphics[Arrow[{{2,0},{0,0}},{0,1}]]​​Style["=",40,Bold]​​Graphics[Arrow[{{2,0},{6,0}}]]
    +
    =
    ​
    If you are sitting in a moving car and then throw a football straight upwards, you will see it as traveling this path :
    ListLinePlot[Table[{6.2,n},{n,0,5}],PlotRange{{0,6.4},{0,5.2}}]​​
    0
    1
    2
    3
    4
    5
    6
    0
    1
    2
    3
    4
    5
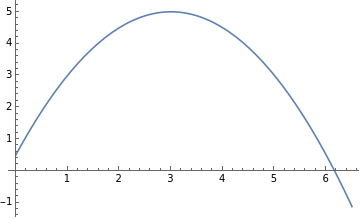
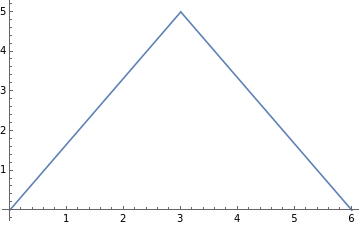
    But a person standing on the sidewalk will see the ball travel a path like :
    Plot[-12
    2
    (x-3)
    +5,{x,0,6.5}]
    The ball gets a velocity added in the horizontal direction for the sidewalk observer, making overall velocity of the ball greater.

    The Speed of Light

    Velocities of objects may add, but this is NOT the case with light. Light has the same velocity (about 300000000 meters/sec) no matter the motion of observers or source.It will always travel at velocity "c".
    ​​ListLinePlot[Table[{6.2,n},{n,0,5}],PlotRange{{0,6.4},{0,5.2}}]
    0
    1
    2
    3
    4
    5
    6
    0
    1
    2
    3
    4
    5
    Plot[Piecewise[{{(5/3)x,x<3},{10-(5/3)x,x>3}}],{x,0,6}]​​

    Light Clock in a Car

    Even if our light beam is in a car, it will have the same velocity, but we see that now the sidewalk observer sees it travelling a greater distance.
    Since Distance = (Rate) * (Time), and rate is the same always, then for a larger distance, time must be larger as well. This is time dilataion.
    Graphics[​​{EdgeForm[Thick],White,Triangle[{{0,0},{1,1},{2,0}}],​​Style[Line[{{1,0},{1,1}}],Thick,Red],​​Style[Line[{{-.2,0},{.2,0}}],Thickness[.035],Black],​​Style[Line[{{.8,1},{1.2,1}}],Thickness[.035],Black],​​Style[Line[{{1.8,0},{2.2,0}}],Thickness[.035],Black],​​Rotate[Text[Style["L",15,Bold, Blue],{.95,.4}],90 Degree],​​Rotate[Text[Style["D",15,Bold, Blue],{.4,.5}],48Degree],​​Rotate[Text[Style["D",15,Bold, Blue],{1.6,.5}],-48Degree], ​​Text[Style["(velocity of car)*(t')",15, Bold, Blue],{1,-.1}],​​Text[Style["
    2
    D
    =
    2
    L
    +(1/4)​(v*t'
    2
    )
    ",20, Bold, Black],{1,-.5}]}]
    ​
    In one bounce up and down, observer in the car sees light traveling a path 2*L, but an observer on the sidewalk sees it traveling a path 2*D
    What happens when v = 0? What happens when v -> c?
    ​
    We see how the blue one traces out a longer path but is traveling with the same speed, so it should take the light in the blue one longer to bounce up and down once. One “tick” is larger in that frame.