Insert

Sample

The Aristotle’s Wheels Paradox

This notebook explore the physics and mathematics behind the paradox of Aristotle’s Wheels

1. History of the paradox.

In[123]:=

ListAnimate[Import["w.gif"]]

Out[123]=

This story is about paradox mentioned in the Greek work Mechanica, dubiously attributed to Aristotle.
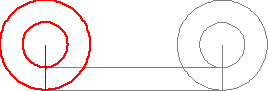
Consider a wheel consisting of two concentric circles of different diameters (that is a wheel within a wheel, or a wheel with external axe). Then if we roll this wheel between two straight lines (at the bottom of each of circle) , we can see than the distance developed by a point of the circle with greater diameter is apparently the same than the distance developed by a point on the small circle. So the wheel should travel the same distance regardless of whether it is rolled from left to right on the top straight line or on the bottom one. This seems to imply that the two circumferences of different sized circles are equal, which is impossible and this is the paradox.

We are going to explain the paradox visually coding the draw of graphics step by step.

2. Visualization of the paradox .

STEP #1. First of all we draw a simple circle with radius 1 centered at the initial rectangular coordinates C{

} = {0,0}:

In[59]:=

Graphics[Circle[{0,0},1]]

Out[59]=

◼

STEP #2. After that we mark the center of the circle with a little black disk:

In[25]:=

Graphics[{Disk[{0,0},0.04],Circle[{0,0},1]}]

Out[25]=

STEP #3. Now we draw a small concentric circle with a radius between 0 and 1 than we can manipulate with a control slider:

In[24]:=

Manipulate[Graphics[{Disk[{0,0},0.04],Circle[{0,0},1],Circle[{0,0},rsmall]}],{rsmall,0,1,0.1}]

Out[24]=

rsmall

STEP #4. We plot two straight lines. One blue at the bottom of the great wheel from (0,-1) to (2π,-1) , and the other red from the bottom of the small wheel from (0,-r_small) to (2π-r_small):

In[26]:=

Manipulate[Graphics[{Disk[{0,0},0.04],Circle[{0,0},1],Circle[{0,0},rsmall],Line[{{0,-1},{2Pi,-1}}],Line[{{0,-rsmall},{2Pi,-rsmall}}]}],{rsmall,0,1,0.1}]

Out[26]=

rsmall

STEP #5. Now we plot the same two wheels at the end of the line and for distinguish them make the first one will be styled with colors and more thick than the second one.

In[27]:=

Manipulate[Graphics[{Disk[{0,0},0.04],Style[Circle[{0,0},1],Blue,Thick],Style[Circle[{0,0},rsmall],Red,Thick],Disk[{2Pi,0},0.02],Circle[{2Pi,0},1],Circle[{2Pi,0},rsmall],Line[{{0,-1},{2Pi,-1}}],Line[{{0,-rsmall},{2Pi,-rsmall}}]}],{rsmall,0,1,0.1}]

Out[27]=

rsmall

STEP #6: We fix the range of plotting and we introduce a new parameter, t, to move the center of the two wheels along the lines:

In[28]:=

Manipulate[Graphics[  Disk[{t,0},0.04], Style[Circle[{t,0},1],Blue,Thick], Style[Circle[{t,0},rsmall],Red,Thick], Disk[{2Pi,0},0.02], Circle[{2Pi,0},1], Circle[{2Pi,0},rsmall], Line[{{0,-1},{2Pi,-1}}], Line[{{0,-rsmall},{2Pi,-rsmall}}] , PlotRange{{-1.1,1.1+2Pi},{-1.1,1.1}} ], {rsmall,0,1,0.1},{t,0,2Pi} ]

Out[28]=

rsmall

STEP #7: We draw a radial segment of the wheel:

In[29]:=

Manipulate[Graphics[  Disk[{t,0},0.04], Style[Circle[{t,0},1],Blue,Thick], Style[Circle[{t,0},rsmall],Red,Thick], Style[Line[{{t,0},{t,-1}}],Black,Thick], Disk[{2Pi,0},0.02], Circle[{2Pi,0},1], Circle[{2Pi,0},rsmall], Line[{{0,-1},{2Pi,-1}}], Line[{{0,-rsmall},{2Pi,-rsmall}}] , PlotRange{{-1.1,1.1+2Pi},{-1.1,1.1}} ], {rsmall,0,1,0.1},{t,0,2Pi} ]

STEP #8: We rotate the radius of the wheel an angle θ = ω· t , interpreting the parameter t as the time lapsed during the motion and ω as the angular velocity of the wheel while is rolling.

STEP #9: Now we will paint part of the straights lines with blue and red while the wheels are moving rotating around the center. And for a more realistic animation effect we discolour the angular part covered by the radius on the blue and red circles.

In the animated graphic above we can see it seems than the wheel is rotating, the big circle is travelling the same distance than the smaller circle. But, we know that it is impossible! because the distance traveled by a rotating wheel is given by the expression d = 2 ·π · r, where r is the radius of the wheel. So when the radius of a wheel is smaller than another the distance traveled will be smaller. That is the paradox, and know, coding again, we will expose the explanation of what is really happening with the physical motion of the wheel.

3. Explanation of the paradox.

In conclusion we can deduce that the inner circle of the wheel is not describing a pure rotation over the top line, because is it was rotating the red walking distance would be shorter than the blue one (as we can see observing the motion of the the outside small red circle). But if the inner red circle is not rotating, how kind of motion is doing?

To answer that last question we are going to plot the trajectory of the points of contact with the lines of the different circles:

After visualizing that, we can see clearly that the blue and red trajectories are cycloid (the common form of the family of trochoid curves), but the green curve is a curtate trochoid so it’s no correspond to a pure rotating motion. In conclusion if we force the wheel to rolling purely over the bottom line, the motion of the inner circle is not a rolling motion, it’s must be a mixing of sliding and rotating motion along the top line.

Conclusions

Wikipedia: https://en.wikipedia.org/wiki/Aristotle%27 s_wheel _paradox
Wolfram MathWorld: http://mathworld.wolfram.com/AristotlesWheelParadox.html
Wolfram Demonstration Project: http://demonstrations.wolfram.com/CycloidCurves/

The Aristotle’s Wheels Paradox

1. History of the paradox.

2. Visualization of the paradox .

3. Explanation of the paradox.

Conclusions

References