You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
What is a Manifold?
What is a Manifold?
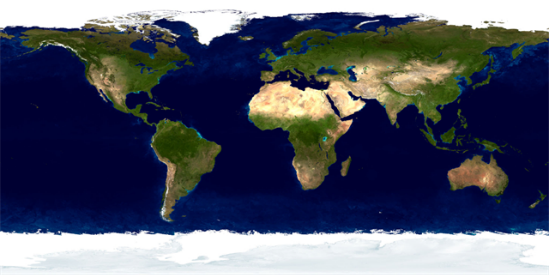
As one begin to study more sophisticated concepts in science, they will encounter the concept of manifold. This weird-sounding wordhave a strong root in mathematics, in particular geometry. Here we will explore what is Manifold intuitively with various example.IntroductionHere we have the world map
This map tries to project the surface of the earth in a rectangular flat surface. Let us compare it to the 3 dimension representation of the earth
Notice the north pole is shown as a big white area which span from America until Asia in the flat map. On the contrary, in 3D-graphic of earth, the north pole is shown as a small white circular area, not even the size of North America.
Taking a look at the actual data
Taking a look at the actual data
,Total@
,
The 3D sphere representation is more accurate. This difference demonstrates how the flat map is not an accurate representation of the earth. We use flat map because we experience the earth as flat surface in our daily experience, but globally it is not correct since it will give some misinformation as we have shown in the case of north pole.This leads us to the intuitive definition of manifolds: something that locally looks like a plane, but globally can be something else. The earth is a manifold.Deformation
First step of understanding Manifold is to think it as a flat plane that gets bent around. Consider this example
Manipulate[Plot3D[k*x*y,{x,-1,1},{y,-1,1},PlotRange{-1,1}],{k,0,1}]
We can see how the flat surface is slowly bent to be the final curvy surface. We will call this bending process as deformation.
Deformation does not have create a smooth surface, nor does it has to produce something with similar size.
Deformation does not have create a smooth surface, nor does it has to produce something with similar size.
Manipulate[Plot3D[Abs[x],{x,y}∈Disk[{0,0},k+1],PlotRange{{-2,2},{-2,2},{0,2}}],{k,0,1}]
Essentially deformation allows us to stretch, fold and bend a surface. However, there are 3 rules that we need to keep in mind:
1). No joining 2 points together
1). No joining 2 points together
rplot[t_]:=RevolutionPlot3D[{Cos[k],Cos[k]*Sin[k],z},{k,0,t},{z,0,1},PlotRange{{-1,1},{-1,1},{0,1}}];Manipulate[rplot[t],{t,1,2π}]
The main reason why we prohibit this because to define deformation mathematically we need to associate each point in flat surface to a point in the deformed surface in one-to-one manner. This can’t happen if we join two points together.
2). No tearing the surface into 2 separate parts
2). No tearing the surface into 2 separate parts
pictureoftearingapart
This is because we want deformation to happen in both directions. If A can be deformed to B, then B can be deformed to A also. If we can tear apart A, then to turn it back we need to glue together some points, which are not allowed.
3). No creating holes
3). No creating holes
Pictureofcreatingholes
In order to deform a holed-surface back, we need to join the boundary together, which is not allowed
Manifold
Anything that is deformable from a surface is a manifold. Here is a deformation of Mt. Everest to flat surface
data=GeoElevationData[GeoDisk[Entity["Mountain","MountEverest"],Quantity[1,"Miles"]]];Manipulate[ListPlot3D[k*data-k*Quantity[22000,"feet"],PlotRange{-1000,7000}],{k,0,1}]
However, to be a manifold, a surface does not need to be deformable globally as long at each point we can define small part of the surface that does.
One example of a surface that is not deformable is a sphere.
One example of a surface that is not deformable is a sphere.
As demonstrated above, to turn a flat circle to a sphere we need to join the boundary points of the circle together, which is not allowed.
However, we can also see that minus a small part on the top, the sphere is deformable to a flat circle. This demonstrate the property of locally deformable, but not globally.
However, we can also see that minus a small part on the top, the sphere is deformable to a flat circle. This demonstrate the property of locally deformable, but not globally.
More Dimension
Even though so far we specify that manifold to be a surface, it doesn’t have to be like that. Here is another example:
A curve is another example of manifold. We call it 1-Manifold, since it is deformed from a line, which is 1 dimension.
In parallel, sphere is a 2-Manifold, since we it is constructed from a surface, which is 2 dimension. In the same spirit, a point is 0-Manifold.
As to be expected, 3-manifold is something that is constructed from a solid 3-dimensional object.
In parallel, sphere is a 2-Manifold, since we it is constructed from a surface, which is 2 dimension. In the same spirit, a point is 0-Manifold.
As to be expected, 3-manifold is something that is constructed from a solid 3-dimensional object.
What is not a Manifold?
What is not a Manifold?
Anything that has a point so that in order to make it from flat object we have to violate the 3 rules we mentioned before is not a manifold.
Two cone stacked together shown above is not a 2-manifold since the point where they are connected is 2 points from both cone joined together, which is not allowed.
The above curve is not a manifold either since it has a self intersecting point.