Backpropagation Algorithm
Backpropagation Algorithm
This topic explains the logic behind the backpropagation functionality in Neural Networks
Preparatory reading
Preparatory reading
Perceptrons
Sigmoid (logistic) function
Sigmoid (logistic) function
The history of backpropagation algorithm
The history of backpropagation algorithm
Backpropagation is a training algorithm for Neural Networks (NN), which allows the training to progress through multiple layers. The basic idea behind neural network computing is the adjustment of neuron weights based on the difference between the result produced by the neuron and the required result. However, the required result is known only for the output layer, which creates a problem for adjusting the weights of hidden layers. For some time, this problem stalled the development of machine learning field. The breakthrough came with the formulation of backpropagation algorithm. The basic idea of backpropagation is 1) to use calculus to assign some of the blame for any training set mistake in the output layer to each neuron in the previous hidden layer; 2) to further split up the blame for the previous hidden layers (if such exist) until the input layer is reached. This method of splitting and assigning the blame is essentially backpropagation of the error.
Backpropagation example
Backpropagation example
As it is clear from the history, backpropagation requires a network with at least one hidden layer. In this example, a three-layer network will be used for a demonstration of the algorithm.
Backpropagating NNs learn by example, that is they require a set of inputs and associated outputs.
Backpropagating NNs learn by example, that is they require a set of inputs and associated outputs.
◼
Initialize an input matrix:
In[55]:=
(x={{0,0,1},{0,1,1},{1,0,1},{1,1,1}});
◼
Initialize an output matrix:
In[56]:=
(y={{0},{1},{1},{0}});
In[57]:=
Grid[{x//MatrixForm,y//MatrixForm}]
Out[57]=
Grid
,
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
0 |
1 |
1 |
0 |
It is easy to see that the problem is basically a logical XOR operation and the third row in the input does not contribute towards the output, however, it makes the problem appear harder. The third input in this case is sometimes called “bias”.
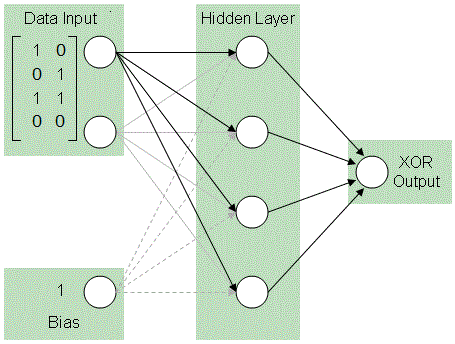
Neural network model
Based on the inputs and output, the network has three input neurons and one output neuron. Generally, the amount of neurons in the hidden layer in this case can be two. However, using four neurons in the hidden layer will allow the network to function almost like a memory bank. This is useful in this example as it will allow to produce XOR output regardless of the value of the third input.
Forward propagation
To demonstrate backpropagation, the network should first complete a first forward propagation and estimate the output.
◼
Since the weights are initiated randomly, it is a good practice to reset the random generator:
In[58]:=
SeedRandom[];
◼
Initialize weights that will be used to generate the inputs to the hidden layer.
weights21 is the weights between the 2nd (hidden) and 1st (input) layers. weights21 is a 3x4 matrix, which connects each 3 input neurons to the 4 hidden neurons:
weights21 is the weights between the 2nd (hidden) and 1st (input) layers. weights21 is a 3x4 matrix, which connects each 3 input neurons to the 4 hidden neurons:
In[80]:=
(weights21=RandomReal[{-1,1},{3,4}]);
◼
weights32 connect 4 hidden neurons to the 1 out neuron, thus they are shaped as 4x1 matrix:
In[81]:=
(weights32=RandomReal[{-1,1},{4,1}]);
The basic formula for feed-forward pass contains two steps.
1) Find the input to the next layer neuron as a sum of the outputs of the previous layer neurons multiplied by weights, in other words a dot-product of the previous layer outputs and weights;
2) Apply the activation function. In this example, logistic sigmoid function is used. Other activation functions also exist, such as TangH, ArcTan, ReLU, etc.
1) Find the input to the next layer neuron as a sum of the outputs of the previous layer neurons multiplied by weights, in other words a dot-product of the previous layer outputs and weights;
2) Apply the activation function. In this example, logistic sigmoid function is used. Other activation functions also exist, such as TangH, ArcTan, ReLU, etc.
◼
Input layer is equal to the input matrix:
In[82]:=
inputs=x;
◼
Compute hidden layer:
In[83]:=
hidden=LogisticSigmoid[inputs.weights21];
◼
Compute output layer - this is the first and very inaccurate approximation of the output:
In[84]:=
outputs=LogisticSigmoid[hidden.weights32]
Out[84]=
{{0.554772},{0.572816},{0.522067},{0.538946}}
Backpropagation
Backpropagation
◼
The first step in backpropagation is to calculate the errors:
In[85]:=
outputsError=y-outputs
Out[85]=
{{-0.554772},{0.427184},{0.477933},{-0.538946}}
Logistic sigmoid
Logistic sigmoid
◼
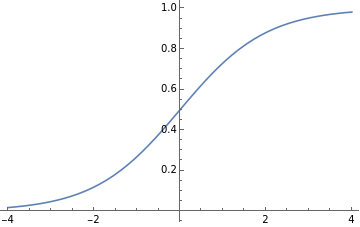
The next step demonstrates the magic of backpropagation and explains the need for the activation function, which is plotted below:
In[86]:=
Plot[LogisticSigmoid[x],{x,-4,4}]
Out[86]=
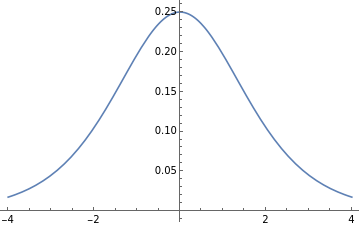
In the forward propagation pass, the values of sigmoid function were applied to the sum of the inputs to the neuron layers. The plot above shows that higher absolute values of x are characterized by sufficiently confident value of y close to 1 or 0. However, the values near x = 0 are close to 0.5 and do not allow a confident prediction. Therefore, these not-confident values must be updated by a higher value. To make such an update, the derivative of the sigmoid function is used (pictured below). The derivative produces higher values of the update coefficient in the area near x = 0 while higher absolute values of x are associated with very small update coefficients.
◼
The values of the derivative of the sigmoid function:
In[87]:=
Plot[LogisticSigmoid'[x],{x,-4,4}]
Out[87]=
Backpropagating errors
Backpropagating errors
◼
Find the update value for the weights between the output and the hidden layers using the derivative of the sigmoid to update the non-confident predictions most heavily:
outputsDelta=outputsError*LogisticSigmoid'[outputs];
◼
For the hidden layer, the errors cannot be calculated because there is no information about what the values of the neurons in this layer should be. Instead, these errors are estimated based on the values of the required update between the output and the hidden layer:
hiddenError=outputsDelta.Transpose[weights32];
◼
The update for the weights in the hidden layer is also estimated using the derivative of the sigmoid function:
hiddenDelta=hiddenError*LogisticSigmoid'[hidden];
◼
Finally, the weights are updated based on the values of the previous layer and the update values:
weights32+=Transpose[hidden].outputsDelta;weights21+=Transpose[inputs].hiddenDelta;
The recalculated weights are used again to calculate the next forward propagation step. The process is repeated until the error in the output layer is sufficiently small or until the allowed number of iterations has been reached (the latter may be necessary for the problems that do not arrive at a high precision solution.
Working example
Working example
◼
Below, all the code from the previous section is put together in a training cycle, which runs for 10000 iterations:
In[73]:=
For[j=0,j<10000,j++,(inputs=x;hidden=LogisticSigmoid[inputs.weights21];outputs=LogisticSigmoid[hidden.weights32];outputsError=y-outputs;outputsDelta=outputsError*LogisticSigmoid'[outputs];hiddenError=outputsDelta.Transpose[weights32];hiddenDelta=hiddenError*LogisticSigmoid'[hidden];weights32+=Transpose[hidden].outputsDelta;weights21+=Transpose[inputs].hiddenDelta;);If[Mod[j,1000]0,Print[outputs],Nothing]]
{{0.0615675},{0.00268832},{0.00282266},{0.000141439}}
{{0.378139},{0.816877},{0.763231},{0.451658}}
{{0.0608943},{0.812021},{0.807389},{0.00448539}}
{{0.0157703},{0.841884},{0.844807},{0.000481342}}
{{0.0162652},{0.898359},{0.899959},{0.000638657}}
{{0.0851205},{0.938234},{0.939068},{0.109775}}
{{0.0511362},{0.954862},{0.955276},{0.0584499}}
◼
The last output produces a fairly good estimate of the desired XOR output. This result is achieved with the following weights:
Application of the trained network
Application of the trained network
◼
Create forward-propagating function (propagating through 2 layers, thus applying the activation function and weights twice):
◼
Use different combinations of inputs to predict the output:
Further Explorations
Neural Networks
Machine Learning
Gradient descent
Authorship information
Tetyana Loskutova
23 June 2017
tetyana.loskutova@gmail.com