Artificial life and cellular automata : Langton’s Ant
Artificial life and cellular automata : Langton’s Ant
Cellular automata are a fascinating gateway to the NKS described by Stephen Wolfram. Only defined by simple rules, they can show the most complex behaviors. In this perspective, Christopher Langton’s “ant” cellular automaton gives a great example of emergence through these simple instructions, questioning the possibility of artificial life.
The rules
The rules
Langton’s ant is a 4-state Turing machine in two dimensions. Let’s consider an infinite grid, whose squares can be either white (default color) or black, and a moving dot, the “ant”
In[15]:=
Ant[x_:{0,0},o_:I]:=With[{y=-.05,m=RotationMatrix[-Arg[o]]},{Red,Circle[x+{0,0},.5],Disk[x+m.{0,.3+y},.07],Disk[x+m.{0,.09+y},Abs[m.({.07,.1}1.4)]],Disk[x+m.{0,-.15+y},Abs[m.({.08,.1}1.4)]],{Line[{x+m.{0,.3+y},x+m.{-.1#,.4+y}}],Line[{x+m.{0,0.05},x+m.{.2#,.15}}],Line[{x+m.{0,.05},x+m.{.22#,.05}}],Line[{x+m.{0,0.05},x+m.{.2#,-.05}}],}&/@{-1,1}}]Show[Graphics[Ant[{5,5}]],AspectRatioAutomatic]
Out[16]=
◼
When the ant leaves a cell, it changes color
◼
If the ant is on a black square it rotates 90° right and move ahead one square
◼
If the ant is on a white square it rotates 90° left and move ahead one square
In[17]:=
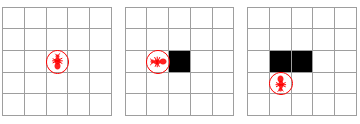
Show[GraphicsGrid[Partition[LangtonsAntPlot[LangtonsAnt[{5,5},{3,3},{0,2}]],3]]]
Out[17]=
In[18]:=
TM2DStep[rule_,{s_,tape_,r:{x_,y_}}]:=Apply[{#1,ReplacePart[tape,#2,{r}],r+#3}&,{s,tape〚x,y〛}/.rule]
Let’s define the moving rule for the ant :
In[19]:=
LangtonsAnt[size_List,x_List,g_List]:=Take[NestList[TM2DStep[{s_,c_}With[{sp=s(2c-1)},{sp,1-c,{Re[sp],Im[sp]}}],#]&,{1,Table[0,{size[[1]]},{size[[2]]}],x},Last[g]],g+1]LangtonsAnt[size_Integer,x_List,its_List]:=LangtonsAnt[{size,size},x,its]LangtonsAnt[size_,x_List,it_Integer]:=LangtonsAnt[size,x,{it,it}]
In[24]:=
Then the plot for the ant:
In[22]:=
LangtonsAntPlot[l_List,opts___]:=Module[{ant=Ant/.{opts}/.Options[LangtonsAnt]},ArrayPlot[#[[2]],Sequence@@DeleteCases[{opts},Ant_],MeshTrue,AspectRatioAutomatic,FrameFalse,DataReversedTrue,EpilogIf[ant,Ant[Reverse[#[[3]]]+{-1,-1}.5,#[[1]]],{}]]&/@l];Options[LangtonsAnt]={AntTrue};
In[23]:=
Emergence of the “highway”
Emergence of the “highway”
If we let the cellular automaton run for a large enough (but still finite) number of steps, we observe the repetition of a pattern.
In[24]:=
size={45,75};Animate[Show[LangtonsAntPlot[LangtonsAnt[size,{24,31},step],MeshStyle{GrayLevel[.7]}]],{step,0,10800,1},AnimationRunningFalse]
Out[25]=
This self-reproducing pattern was called by Langton the “Highway” : no matter the initial conditions of the grid, the position of the ant or the actual number of ants involved, it will appear at some finite number of steps. This kind of behavior was classified as one of the first “emergence” pattern discovered in the computational universe.
Further Explorations
Emergence
Langton’s ant
Cellular automata
Langton’s ant
Cellular automata
Authorship information
Théo Beigbeder
June/July 2017
theo.arthur.beigbeder@gmail.com