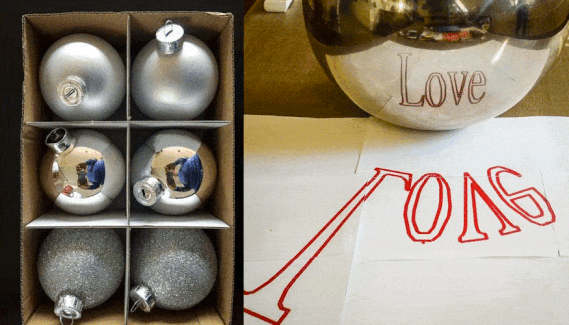Anamorphic Reflections in a Christmas Ball
Anamorphic Reflections in a Christmas Ball
I recently got inspired by a sculpture sold on Saatchi Art featuring anamorphic deformation by reflection in a spherical mirror. Being curious and interested in anamorphic transformations, I wanted to build something similar and find the math behind it using Mathematica...
A plain, undecorated Christmas ball can serve as a perfect convex spherical mirror to test some of our physics and coding skills. I used a 7 cm XMas ball now dumped in stores for Euro1.75 a sixpack! In a nutshell: I wanted to see how a deformed text should look like in order to show up undeformed when reflected in a ball shaped mirror.
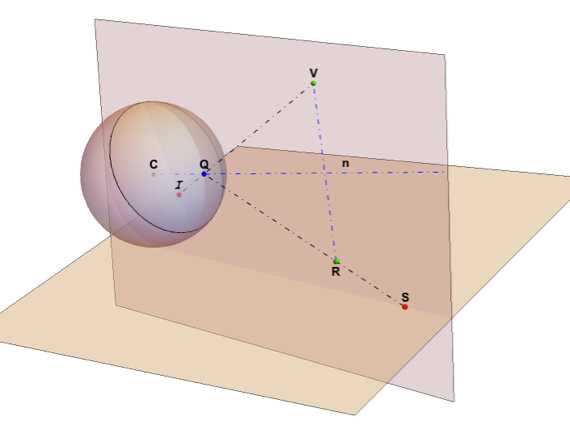
The graphics below show a spherical mirror centered at C:(0,0,0), our eye at viewpoint V: (xv,0,zv) and a reflected point S on the base plane beneath the ball. One of the reflected light rays leaving S will meet the mirror at Q such that its reflection meets the eye at V. But the eye at V will now perceive the point S at I.
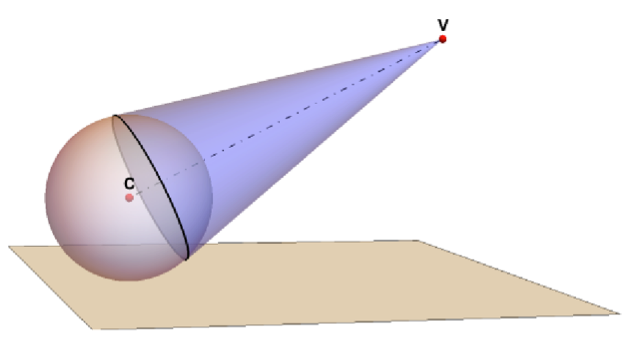
I is a perceived image point inside the view disk perpendicular to VC. According to the law of reflection, the lines VQI and SRQ will form equal angles with the normal n to the sphere in Q. All image points will be restricted to a disk that is the base of the view cone with the line CV as axis and an opening angle of tan^-1(zv/xv). This image disk is at an offset 1/xv from C and has a radius of Sqrt[1-(1/xv)^2].
The point Q (q1, q2, q3) is the intersection of the view line VI and the mirror sphere. It can be computed by solving this equation:
solQ=NSolve[Element[{x,y,z},HalfLine[{imagePointI,viewPointV}]]&&Element[{x,y,z},Sphere[]],{x,y,z}];pointQ=First[{x,y,z}/.solQ];{q1,q2,q3}=pointQ;
The points C, Q, I, V and S are all in the same plane. We have R, the projection of V to the normal n.
projectionPlane=InfinitePlane[pointQ,{pointQ,viewPointV}];reflectionPt=2Projection[viewPointV,pointQ]-viewPointV;
The point S is now the intersection of of the line QR with the base plane. It can be computed by solving this equation:
solS=NSolve[{{x,y,z}∈HalfLine[{{q1,q2,q3},reflectionPt}]&&{x,y,z}∈InfinitePlane[{{0,0,-1},{0,1,-1},{0,-1,-1}}]},{x,y,z}];
After simplification, we can write the following function that maps the perceived image point I to the reflected point R :
xmasBallMap[iPt:{yi_,zi_},vPt:{xv_,zv_}]:=Module[{imagePtRotated,solQ,q1,q2,q3},(*imagepointinreal(rotated)pane*)imagePtRotated={(1-zizv)/Norm@vPt,yi,(xv^2zi+zv)/xv/Norm@vPt};(*intersectionviewline-sphere:Q*)solQ=NSolve[Element[{x,y,z},HalfLine[{imagePtRotated,{xv,0,zv}}]]&&Element[{x,y,z},Sphere[]],{x,y,z}];{q1,q2,q3}=First[{x,y,z}/.solQ];Join[{-(1+q3)(q2^2+q3^2)xv+q1^2(xv-q3xv)+q1^3(-1+zv)+q1q2^2(-1+zv)+q1q3(q3(-1+zv)+2zv),q2(2q1xv+q1^2(-1+zv)+q2^2(-1+zv)+q3(q3(-1+zv)+2zv))}/(-2q1q3xv+q3^2(q3-zv)+q1^2(q3+zv)+q2^2(q3+zv)),{-1}]]
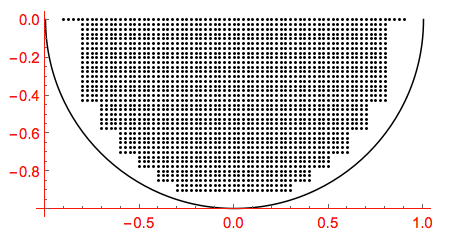
All possible image points have to fit inside the lower half-disk. This is a grid of image points inside the view disk:
pts=Table[Table[{x,y},{x,-Floor[Sqrt[1-y^2],.1]+.1,Floor[Sqrt[1-y^2],.1]-.1,.025}],{y,0,-.9,-.025}];viewDisk=Graphics[{Circle[{0,0},1,{π,2.π}],{AbsolutePointSize[2],Point/@pts}},AxesTrue,AxesOrigin{-1,-1},AxesStyleDirective[Thin,Red]]
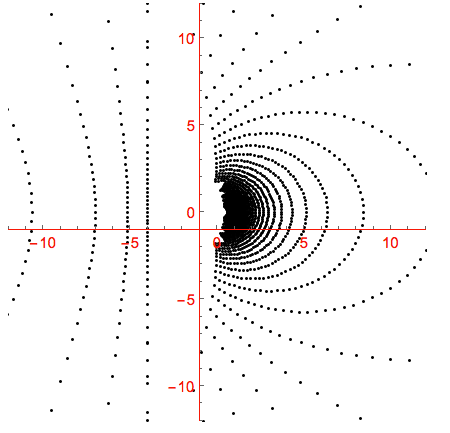
This is the reflected spherical anamorphic map of these points:
We can see that there is a large magnification between the perceived image inside the ball and it reflected image. Getting a point too close to the rim of the view disk will project its reflection far away. This GIF shows the function in action. The image point I follows a circle in the perceived image disk while its reflection S follows the closed curve of its map xmasBallmap(I, v) in the base plane.
We can now further test our function with some text e.g.: “[MathematicaIcon]Mathematica[MathematicaIcon]”.
The text image needs to be rescaled and centered to fit inside the ball.
This shows the text as should be perceived in the lower half of the mirror sphere:
This is the code for a 3D view of the complete setup: the spherical mirror, the perceived text in the disk inside the sphere and the deformed, anamorphic image on the base plane.
Time to try the real thing. This shows a 7cm diameter XMas ball mirror with the text reflected in it.
Get yourself a nice reflecting Christmas ball and this is a pdf for you to printout and try it! (see attached pdf file for printing)